课堂内容

二分图匹配

Hall 定理

假设 $G = (X,Y,E)$ 是一个二分图，且 $|X| \le |Y|$ 。对于 $W \subseteq X$ ，记 $N_{G}(W)$ 表示在图 $G$ 中所有与集合 $W$ 中的点相邻的点的集合。那么 $X$ 的完美匹配存在，当且仅当 $|W| \le |N_G(W)|$ 对于所有 $W \subseteq X$ 存在。

匈牙利算法

不断搜索增广路，每次考虑一条增广路，看看把一个匹配拆了能否增加一个新的匹配。

模板代码：Link

网络最大流算法

Dinic

Dinic 是求解网络最大流的其中一个算法，也是最常用的算法。其核心思想为：每次用 BFS 寻找增广路，然后用 DFS 统计增广路上的最大流量。但是这样会有一些问题，如果给定的网络是如下情况的话：

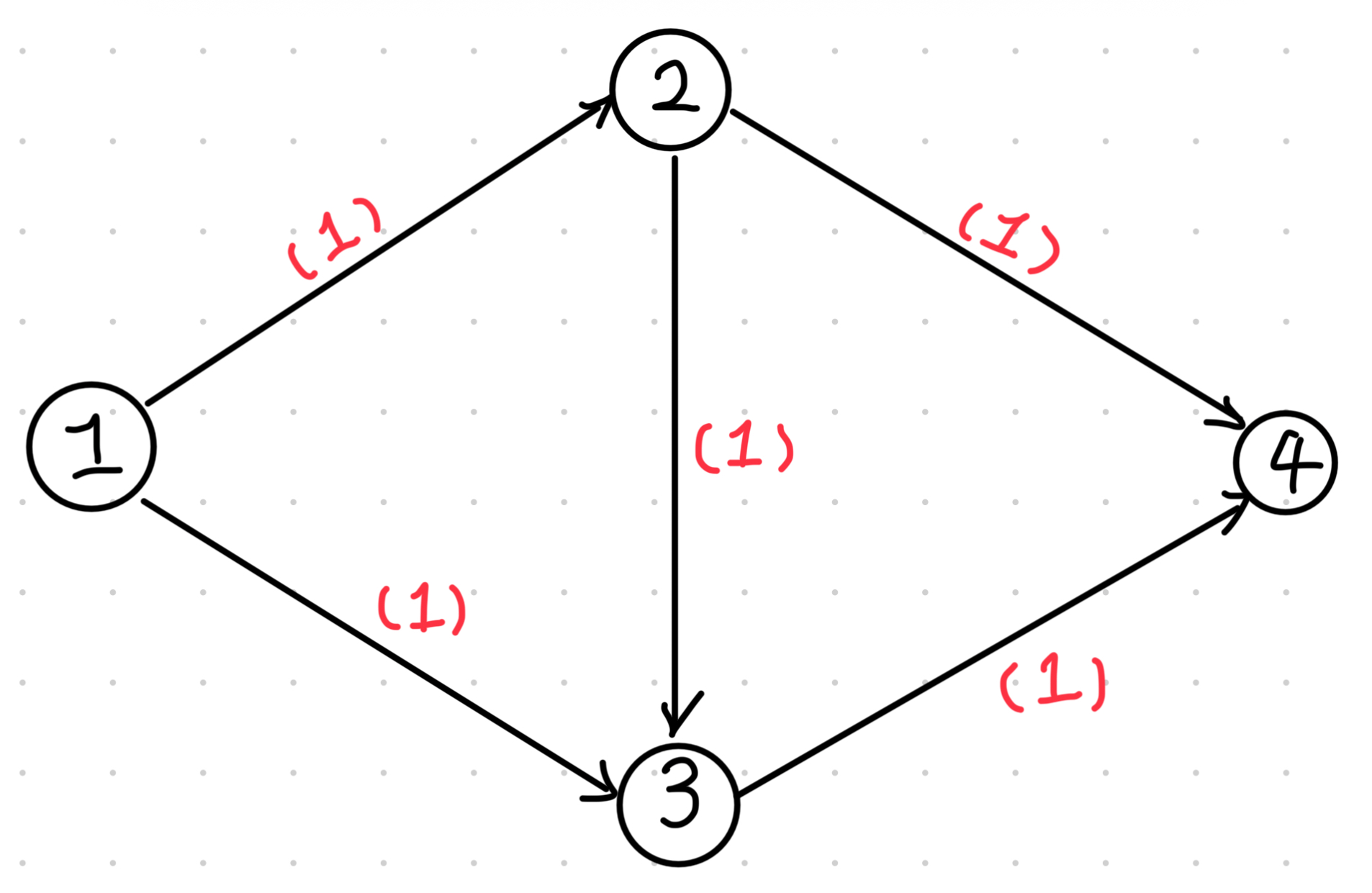
如果直接按照上面说的方法走，第一次增广路可能是 $1 \to 2 \to 3 \to 4$ ，但实际上最优的是 $1 \to 2 \to 4$ 和 $1 \to 3 \to 4$ 。所以为了解决这个问题，我们需要对原图的所有边建立反向边 $(v,u,0)$ 。如果我们选择了这条路，则将其反向边的流量减去我们现在流过这条边的流量，这样可以做到类似反悔贪心的效果。